VizualBusiness: Multiple recurrence and convergence results associated to F

Multiple recurrence and convergence results associated to F_p^omega-actions:
Vitaly Bergelson, Tamar Ziegler, and I have just uploaded to the arXiv our joint paper “Multiple recurrence and convergence results associated to ${{\bf F}_{p}^{\omega}}$ -actions“. This paper is primarily concerned with limit formulae in the theory of multiple recurrence in ergodic theory. Perhaps the most basic formula of this type is the mean ergodic theorem, which (among other things) asserts that if ${(X,{\mathcal X}, \mu,T)}$ is a measure-preserving ${{\bf Z}}$ -system (which, in this post, means that ${(X,{\mathcal X}, \mu)}$ is a probability space and ${T: X \mapsto X}$ is measure-preserving and invertible, thus giving an action ${(T^n)_{n \in {\bf Z}}}$ of the integers), and ${f,g \in L^2(X,{\mathcal X}, \mu)}$ are functions, and ${X}$ 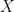is ergodic (which means that ${L^2(X,{\mathcal X}, \mu)}$ contains no ${T}$ -invariant functions other than the constants (up to almost everywhere equivalence, of course)), then the average

$\displaystyle \frac{1}{N} \sum_{n=1}^N \int_X f(x) g(T^n x)\ d\mu \ \ \ \ \ (1)$

converges as ${N \rightarrow \infty}$ to the expression

$\displaystyle (\int_X f(x)\ d\mu) (\int_X g(x)\ d\mu);$

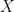
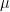
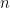
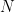
see e.g. this previous blog post. Informally, one can interpret this limit formula as an equidistribution result: if ${x}$ is drawn at random from ${X}$ (using the probability measure ${\mu}$ ), and ${n}$ is drawn at random from ${\{1,\ldots,N\}}$ for some large ${N}$ , then the pair ${(x, T^n x)}$ becomes uniformly distributed in the product space ${X \times X}$ (using product measure ${\mu \times \mu}$ ) in the limit as ${N \rightarrow \infty}$ .
If we allow ${(X,\mu)}$ to be non-ergodic, then we still have a limit formula, but it is a bit more complicated. Let ${{\mathcal X}^T}$ be the ${T}$ -invariant measurable sets in ${{\mathcal X}}$ ; the ${{\bf Z}}$ -system ${(X, {\mathcal X}^T, \mu, T)}$ can then be viewed as a factor of the original system ${(X, {\mathcal X}, \mu, T)}$ , which is equivalent (in the sense of measure-preserving systems) to a trivial system ${(Z_0, {\mathcal Z}_0, \mu_{Z_0}, 1)}$ (known as the invariant factor) in which the shift is trivial. There is then a projection map ${\pi_0: X \rightarrow Z_0}$ to the invariant factor which is a factor map, and the average (1) converges in the limit to the expression

$\displaystyle \int_{Z_0} (\pi_0)_* f(z) (\pi_0)_* g(z)\ d\mu_{Z_0}(x), \ \ \ \ \ (2)$

where ${(\pi_0)_*: L^2(X,{\mathcal X},\mu) \rightarrow L^2(Z_0,{\mathcal Z}_0,\mu_{Z_0})}$ is the pushforward map associated to the map ${\pi_0: X \rightarrow Z_0}$ ; see e.g. this previous blog post. We can interpret this as an equidistribution result. If ${(x,T^n x)}$ is a pair as before, then we no longer expect complete equidistribution in ${X \times X}$ in the non-ergodic, because there are now non-trivial constraints relating ${x}$ with ${T^n x}$ ; indeed, for any ${T}$ -invariant function ${f: X \rightarrow {\bf C}}$ , we have the constraint ${f(x) = f(T^n x)}$ ; putting all these constraints together we see that ${\pi_0(x) = \pi_0(T^n x)}$ (for almost every ${x}$ , at least). The limit (2) can be viewed as an assertion that this constraint ${\pi_0(x) = \pi_0(T^n x)}$ are in some sense the “only” constraints between ${x}$ and ${T^n x}$ , and that the pair ${(x,T^n x)}$ is uniformly distributed relative to these constraints.

Limit formulae are known for multiple ergodic averages as well, although the statement becomes more complicated. For instance, consider the expression

$\displaystyle \frac{1}{N} \sum_{n=1}^N \int_X f(x) g(T^n x) h(T^{2n} x)\ d\mu \ \ \ \ \ (3)$

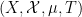
for three functions ${f,g,h \in L^\infty(X, {\mathcal X}, \mu)}$ ; this is analogous to the combinatorial task of counting length three progressions in various sets. For simplicity we assume the system ${(X,{\mathcal X},\mu,T)}$ to be ergodic. Naively one might expect this limit to then converge to

$\displaystyle (\int_X f\ d\mu) (\int_X g\ d\mu) (\int_X h\ d\mu)$

which would roughly speaking correspond to an assertion that the triplet ${(x,T^n x, T^{2n} x)}$ is asymptotically equidistributed in ${X \times X \times X}$ . However, even in the ergodic case there can be additional constraints on this triplet that cannot be seen at the level of the individual pairs ${(x,T^n x)}$ , ${(x, T^{2n} x)}$ . 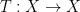The key obstruction here is that of eigenfunctions of the shift ${T: X \rightarrow X}$ , that is to say non-trivial functions ${f: X \rightarrow S^1}$ that obey the eigenfunction equation ${Tf = \lambda f}$ almost everywhere for some constant (or ${T}$ -invariant) ${\lambda}$ . Each such eigenfunction generates a constraint

$\displaystyle f(x) \overline{f(T^n x)}^2 f(T^{2n} x) = 1 \ \ \ \ \ (4)$

tying together ${x}$ , ${T^n x}$ , and ${T^{2n} x}$ . However, it turns out that these are in some sense the only constraints on ${x,T^n x, T^{2n} x}$ that are relevant for the limit (3). More precisely, if one sets ${{\mathcal X}_1}$ to be the sub-algebra of ${{\mathcal X}}$ generated by the eigenfunctions of ${T}$ , then it turns out that the factor ${(X, {\mathcal X}_1, \mu, T)}$ is isomorphic to a shift system ${(Z_1, {\mathcal Z}_1, \mu_{Z_1}, x \mapsto x+\alpha)}$ known as the Kronecker factor, for some compact abelian group ${Z_1 = (Z_1,+)}$ and some (irrational) shift ${\alpha \in Z_1}$ ; the factor map ${\pi_1: X \rightarrow Z_1}$ pushes eigenfunctions forward to (affine) characters on ${Z_1}$ . It is then known that the limit of (3) is

$\displaystyle \int_\Sigma (\pi_1)_* f(x_0) (\pi_1)_* g(x_1) (\pi_1)_* h(x_2)\ d\mu_\Sigma$

where ${\Sigma \subset Z_1^3}$ is the closed subgroup

$\displaystyle \Sigma = \{ (x_1,x_2,x_3) \in Z_1^3: x_1-2x_2+x_3=0 \}$

and ${\mu_\Sigma}$ is the Haar probability measure on ${\Sigma}$ ; see this previous blog post. The equation ${x_1-2x_2+x_3=0}$ defining ${\Sigma}$ corresponds to the constraint (4) mentioned earlier. Among other things, this limit formula implies Roth’s theorem, which in the context of ergodic theory is the assertion that the limit (or at least the limit inferior) of (3) is positive when ${f=g=h}$ is non-negative and not identically vanishing.
If one considers a quadruple average

$\displaystyle \frac{1}{N} \sum_{n=1}^N \int_X f(x) g(T^n x) h(T^{2n} x) k(T^{3n} x)\ d\mu \ \ \ \ \ (5)$

(analogous to counting length four progressions) then the situation becomes more complicated still, even in the ergodic case. In addition to the (linear) eigenfunctions that already showed up in the computation of the triple average (3), a new type of constraint also arises from quadratic eigenfunctions ${f: X \rightarrow S^1}$ , which obey an eigenfunction equation ${Tf = \lambda f}$ in which ${\lambda}$ is no longer constant, but is now a linear eigenfunction. 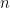For such functions, ${f(T^n x)}$ behaves quadratically in ${n}$ , and one can compute the existence of a constraint

$\displaystyle f(x) \overline{f(T^n x)}^3 f(T^{2n} x)^3 \overline{f(T^{3n} x)} = 1 \ \ \ \ \ (6)$

between ${x}$ , ${T^n x}$ , ${T^{2n} x}$ , and ${T^{3n} x}$ that is not detected at the triple average level. As it turns out, this is not the only type of constraint relevant for (5); there is a more general class of constraint involving two-step nilsystems which we will not detail here, but see e.g. this previous blog post for more discussion. Nevertheless there is still a similar limit formula to previous examples, involving a special factor ${(Z_2, {\mathcal Z}_2, \mu_{Z_2}, S)}$ which turns out to be an inverse limit of two-step nilsystems; this limit theorem can be extracted from the structural theory in this paper of Host and Kra combined with a limit formula for nilsystems obtained by Lesigne, but will not be reproduced here. The pattern continues to higher averages (and higher step nilsystems); this was first done explicitly by Ziegler, and can also in principle be extracted from the structural theory of Host-Kra combined with nilsystem equidistribution results of Leibman. These sorts of limit formulae can lead to various recurrence results refining Roth’s theorem in various ways; see this paper of Bergelson, Host, and Kra for some examples of this.

The above discussion was concerned with ${{\bf Z}}$ -systems, but one can adapt much of the theory to measure-preserving ${G}$ -systems for other discrete countable abelian groups ${G}$ , in which one now has a family ${(T_g)_{g \in G}}$ of shifts indexed by ${G}$ rather than a single shift, obeying the compatibility relation ${T_{g+h}=T_g T_h}$ . The role of the intervals ${\{1,\ldots,N\}}$ in this more general setting is replaced by that of Folner sequences. For arbitrary countable abelian ${G}$ , the theory for double averages (1) and triple limits (3) is essentially identical to the ${{\bf Z}}$ -system case. But when one turns to quadruple and higher limits, the situation becomes more complicated (and, for arbitrary ${G}$ , still not fully understood). However one model case which is now well understood is the finite field case when ${G = {\bf F}_p^\omega = \bigcup_{n=1}^\infty {\bf F}_p^n}$ is an infinite-dimensional vector space over a finite field ${{\bf F}_p}$ (with the finite subspaces ${{\bf F}_p^n}$ then being a good choice for the Folner sequence). Here, the analogue of the structural theory of Host and Kra was worked out by Vitaly, Tamar, and myself in these previous papers (treating the high characteristic and low characteristic cases respectively). In the finite field setting, it turns out that nilsystems no longer appear, and one only needs to deal with linear, quadratic, and higher order eigenfunctions (known collectively as phase polynomials). 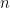It is then natural to look for a limit formula that asserts, roughly speaking, that if ${x}$ is drawn at random from a ${{\bf F}_p^\omega}$ -system and ${n}$ drawn randomly from a large subspace of ${{\bf F}_p^\omega}$ , then the only constraints between ${x, T^n x, \ldots, T^{(p-1)n} x}$ are those that arise from phase polynomials. The main theorem of this paper is to establish this limit formula (which, again, is a little complicated to state explicitly and will not be done here). In particular, we establish for the first time that the limit actually exists (a result which, for ${{\bf Z}}$ -systems, was one of the main results of this paper of Host and Kra).

As a consequence, we can recover finite field analogues of most of the results of Bergelson-Host-Kra, though interestingly some of the counterexamples demonstrating sharpness of their results for ${{\bf Z}}$ -systems (based on Behrend set constructions) do not seem to be present in the finite field setting (cf. this previous blog post on the cap set problem). 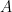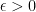In particular, we are able to largely settle the question of when one has a Khintchine-type theorem that asserts that for any measurable set ${A}$ in an ergodic ${{\bf F}_p^\omega}$ -system and any ${\epsilon>0}$ , one has

$\displaystyle \mu( T_{c_1 n} A \cap \ldots \cap T_{c_k n} A ) > \mu(A)^k - \epsilon$

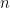
for a syndetic set of ${n}$ , where ${c_1,\ldots,c_k \in {\bf F}_p}$ are distinct residue classes. 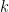It turns out that Khintchine-type theorems always hold for ${k=1,2,3}$ (and for ${k=1,2}$ ergodicity is not required), and for ${k=4}$ it holds whenever ${c_1,c_2,c_3,c_4}$ form a parallelogram, but not otherwise (though the counterexample here was such a painful computation that we ended up removing it from the paper, and may end up putting it online somewhere instead), and for larger ${k}$ we could show that the Khintchine property failed for generic choices of ${c_1,\ldots,c_k}$ , though the problem of determining exactly the tuples for which the Khintchine property failed looked to be rather messy and we did not completely settle it.

Filed under: math.DS, paper Tagged: ergodic theory, finite fields, multiple convergence, multiple recurrence, polynomials, Tamar Ziegler, Vitaly Bergelson

DIGITAL JUICE

VizualBusiness

Saturday, May 25, 2013

Multiple recurrence and convergence results associated to F_p^omega-actions

No comments:

Post a Comment

Digital Juice for Primary Education

About Me

Translate

Total Pageviews