VizualBusiness: What maths A-level doesn’t necessarily give you

What maths A-level doesn’t necessarily give you:
I had a mathematical conversation yesterday with a 17-year-old boy who is in his second year of doing maths A-level. Although a sample of size 1 should be treated with caution, I’m pretty sure that the boy in question, who is very intelligent and is expected to get at least an A grade, has been taught as well as the vast majority of A-level mathematicians. If this is right, then what I discovered from talking to him was quite worrying.
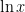
The purpose of the conversation was to help him catch up with some work that he had missed through illness. The particular topics he wanted me to cover were integrating $\log x$ , or $\ln x$ as he called it, and integration by parts. (Actually, after I had explained integration by parts to him, he told me that that hadn’t been what he had meant, but I don’t think any harm was done.) But as we were starting, he asked me why the derivative of $e^x$ was $e^x$ , and what was special about $e$ .

That seemed like a good preliminary conversation to have, so I said, “OK, let’s try to differentiate $e^x$ from first principles and see what happens.” He didn’t know what I meant by “from first principles” so I tried to give him a nudge, by saying, “If you didn’t know the derivative of $e^x$ , then how would you go about working it out?”
At this point, he suggested $xe^{x-1}$ . To be fair to him, he wasn’t saying that he knew that this was correct. Nevertheless, this was an interesting piece of cognitive dissonance, given that we were trying to understand why the derivative of $e^x$ was $e^x$ . But what bothered me more than the fact that he said it was the fact that he couldn’t see why it wasn’t right. 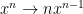And what bothered me perhaps even more than that was the fact that he should think of “from first principles” as mechanically applying the $x^n\rightarrow nx^{n-1}$ rule.
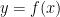
In an effort to get past that, I asked, “Yes, but what does the derivative actually mean?” He had no answer. So I drew a graph of an arbitraryish function, labelled it $y=f(x)$ , drew a point on the curve, and asked him what the derivative meant. I think he did then say that it was the gradient of the curve at that point. (I don’t think he used the word “tangent”.) I asked how we could go about working that out. He suggested $y/x$ . 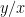I said, “So to work out the derivative you just divide by $x$ — is that it?” He laughed and said no.
It was time to go back to basics, so I asked him how you work out the gradient of a straight line. He said, “Rise over run”, terminology that I either never knew or had completely forgotten — but the meaning was obvious. I then asked what the difficulty was when the line wasn’t straight, to which he replied that the gradient was changing all the time. So what could we do about that? He suggested taking a point not too far away and working out the slope of the line joining that to the point in question.
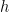
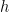
Now we were getting somewhere. I had already drawn a line segment going up from a point on the x-axis marked $x$ until it hit the curve. I did the same for a line segment going up from a point marked $x+h$ and asked what the rise and run were. He correctly got the answers $f(x+h)-f(x)$ and $h$ . I then said that as $h$ got smaller and smaller, the curve got more and more straight, so
$\displaystyle \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}h$
was a formula for the derivative $f'(x)$ .
“Have you really never seen that before?” I asked. He denied it, but when I pressed him, he eventually conceded that he probably had seen it, but that if so, then it would have been clearly flagged up as something that he didn’t need to know, because there wouldn’t be questions about it on the exam.
It’s that that bothered me enough to make me need to get it off my chest in the form of a blog post. It hardly needs spelling out what was wrong with the argument that his teacher gave (if his teacher did in fact give that argument — I cannot be certain about this, though the mere fact that that was the message that got across is bad enough) but I’m going to anyway. Let’s suppose that your aim is simply to do well at maths A-level and that there are no questions that test your familiarity with the formula for the derivative of an arbitrary (nice) function at an arbitrary point. Which is better?
1. Don’t make any effort to learn and understand the formula, but simply learn a few basic examples of derivatives (polynomials, exponentials, logs, trig functions) and rules for differentiating combinations (linearity, product rule, quotient rule, chain rule) and you should be able to differentiate anything that comes up in the exams.
2. Learn what the derivative means, derive the formula for the derivative of an arbitrary function at an arbitrary point, calculate a few derivatives from first principles, derive the product rule, quotient rule and chain rule, and then learn how to use them to differentiate combinations.
The answer is that if you are capable of doing 2, then 2 is far better. And the boy I was talking to was certainly capable of doing 2. Why is it better? Because (and this is something I plan to devote a blog post to at some point) memory works far better when you learn networks of facts rather than facts in isolation. If you don’t really understand what differentiation is all about, then the fact that the derivative of $x^3$ is $3x^2$ is a completely different fact from the fact that the derivative of $e^x$ is $e^x$ . But if you’ve derived them both from first principles (I’ll come back to what I said about $e^x$ in a moment), then they are related: we have a process we do to the functions $x^3$ and $e^x$ and this is what comes out. Of course, another reason is that if you forget something, you have a chance of rederiving it, but that’s a slightly different point. Your knowledge of a piece of maths is far more grounded if you know how it is derived, or at least have some memory of the derivation, even if you have no problem remembering the fact in question. Even if you forget the details of the derivations, just having seen them has a major effect on binding together the facts you know.
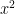
After I had explained differentiation in the abstract, I suggested that we should try differentiating $x^2$ from first principles. Or as I put it, “Let’s apply this formula in the case $f(x)=x^2$ . What do we get then?” To my further dismay, he didn’t immediately know what to do. “If $f(x)=x^2$ , then what is $f(x+h)$ ?” I asked. I can’t remember what his response was, but it wasn’t $(x+h)^2$ . He floundered and made wild guesses, not really understanding what I was asking. 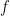Again, something quite serious seemed not to have been done by his school, though I couldn’t give a precise diagnosis in this case — something along the lines of understanding the notion of a function well enough to talk about an abstract function $f$ and see that it could have many instantiations.
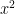
Anyhow, once that point was cleared up (not necessarily for good, but for then anyway) we got through the differentiation of $x^2$ without further trouble. Again he denied having seen that derivation — maybe it was at that point that he said the thing about not needing to know it for the exam.
The general point here is of course that A-levels have got easier and schools have a natural tendency to teach to the test. If just one of those were true, it would be far less of a problem. I would have nothing against an easy A-level if people who were clever enough were given a much deeper understanding than the exam strictly required (though as I’ve argued above, for many people teaching to the test is misguided even on its own terms, since they will do a lot better on the exam if they have not been confined to what’s on the test), and I would not be too against teaching to the test if the test was hard enough.
How about differentiating $e^x$ ? Well, after a couple of false starts we got to the expression
$\displaystyle \lim_{h\to 0}\frac {e^{x+h}-e^x}h$
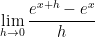
I asked what could be done with $e^{x+h}$ . Quite a bit of prompting was needed to get him to say $e^xe^h$ . Then I asked what could be done with $e^xe^h-e^x$ . A lot of prompting was needed to get the answer to that question. (I had to ask what he would do with $uv-u$ .) Anyhow, we eventually got to
$\displaystyle e^x\lim_{h\to 0}\frac{e^h-1}h$
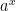
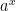
I decided just to point out that the last limit was the derivative of $e^x$ at 0. I also pointed out that the entire argument so far worked just as well for the function $a^x$ , whatever the (positive) value of $a$ . I then drew some pictures for different $a^x$ , pointing out that some of them crossed the y-axis with a slope less than 1 and others with a slope greater than 1 and that $e^x$ was the one where it actually equalled 1. He asked me why the slope was exactly 1 for $e^x$ , which was a good opportunity for me to try to explain that that was getting things the wrong way round, and that $e$ was chosen precisely to make that work. (Of course, the question would make very good sense the way he asked it if we had already defined $e$ in some other way, but I’m not sure he had. Certainly, I remember this as the definition of $e$ when I was at school, and I remember feeling slightly uncomfortable about it.)
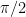
There was plenty more of our conversation, though not much more to say about it. I accidentally fell into a derivation of the product rule, which again I think he had not seen. That was part of my preparation for deriving the formula for integration by parts. When I had done that, I went through an example or two. One of the examples I tried was $x\sin x$ from $0$ to $\pi/2$ . 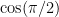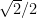(He thought $\cos(\pi/2)$ was $\sqrt{2}/2$ , by the way, but was OK when we did it in degrees.) We got the answer $\int_0^{\pi/2}x\sin xdx=1$ . 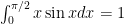I then felt annoyed not to be able to see why the answer had to be 1. I still haven’t got round to thinking about that.
I also discussed integrating $\log x$ by the method I call guess-and-adjust. You guess $x\log x$ because one part of what the product rule gives you is correct and you might be able to deal with the other part. Differentiating you get $\log x + 1$ . “What can we do to get rid of that 1?” He suggested $x\log x -1$ . We tried that, saw why it didn’t work, and then got to the right answer.
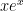
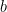
He managed to integrate $xe^x$ between $a$ and $b$ with no help at all, so I think he got the basic idea, though whether he’ll hold on to it I don’t know.
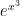
Another thing I discovered was that he was very shaky on the chain rule. When I asked him what the chain rule said, he didn’t know what I was talking about. Eventually I got a glimmer of recognition out of him by writing down $\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$ . But the idea that if you want to differentiate $e^{x^3}$ you first pretend that $x^3$ is a single variable with respect to which you are differentiating and then correct what you’ve just done by multiplying by the derivative of $x^3$ was completely foreign to him. We looked at a few examples but they’ll need reinforcing at some point. It was yet another illustration of the general principle that if you forget about understanding what’s going on and concentrate on mechanical manipulations, you’ll forget how to do even the mechanical manipulations.

DIGITAL JUICE

VizualBusiness

Tuesday, November 20, 2012

What maths A-level doesn’t necessarily give you

No comments:

Post a Comment

Digital Juice for Primary Education

About Me

Translate

Total Pageviews