van Kampen’s theorem via covering spaces:
If
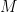
is a connected
topological manifold, and
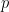
is a point in
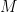
, the (topological)
fundamental group 
of
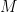
at
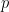
is traditionally defined as the space of equivalence classes of loops starting and ending at
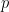
, with two loops considered homotopic if they are equivalent to each other. (One can of course define the fundamental group for more general classes of topological spaces, such as locally path connected spaces, but we will stick with topological manifolds in order to avoid pathologies.) As the name suggests, it is one of the most basic topological invariants of a manifold, which among other things can be used to classify the
covering spaces of that manifold.
One of the basic tools used to compute fundamental groups is
van Kampen’s theorem:
Theorem 1 (van Kampen’s theorem) Let  be connected open sets covering a connected topological manifold
be connected open sets covering a connected topological manifold 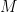 with
with  also connected, and let
also connected, and let 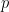 be an element of
be an element of  . Then
. Then  is isomorphic to the amalgamated free product
is isomorphic to the amalgamated free product  .
.
Since the topological fundamental group is customarily defined using loops, it is not surprising that many proofs of van Kampen’s theorem (e.g. the one in
Hatcher’s text) proceed by an analysis of the loops in

, carefully deforming them into combinations of loops in

or in
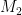
and using the combinatorial description of the amalgamated free product. But I recently learned (thanks to the responses to
this recent MathOverflow question of mine) that by using
Grothendieck’s category theoretic re-interpretation of the fundamental group as the automorphism group of the fibre functor from coverings

of
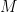
to the fibre

above
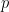
, that one can convert statements about fundamental groups to statements about coverings. In particular, van Kampen’s theorem turns out to be equivalent to a basic statement about how to glue a cover of

and a cover of
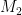
together to give a cover of
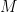
. One advantage of this alternate proof is that it can be extended to other contexts (such as the
étale fundamental groups of varieties or schemes) in which the concept of a path or loop is no longer useful, but for which the notion of a covering is still important. I am thus recording (mostly for my own benefit) the covering-based proof of van Kampen’s theorem in the topological setting below the fold
— 1. Proof of van Kampen theorem —
The proof of van Kampen’s theorem boils down (after using the well-known equivalence of categories between covers of a manifold
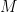
, and sets with an action of the fundamental group) to the following fact about covers:
Proposition 2 (Gluing of covers) Let  be connected open sets covering a connected topological manifold
be connected open sets covering a connected topological manifold 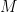 with
with  also connected, and let
also connected, and let 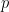 be an element of
be an element of  . If
. If  and
and  are covering maps which become isomorphic upon restricting the base to
are covering maps which become isomorphic upon restricting the base to  , then there is a covering map
, then there is a covering map  which becomes isomorphic to
which becomes isomorphic to 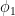 on restricting the base to
on restricting the base to  , and isomorphic to
, and isomorphic to  on restricting the base to
on restricting the base to 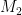 (and with all four isomorphisms forming a commuting square).
(and with all four isomorphisms forming a commuting square).
This proposition is easily verified by gluing together

and

as topological spaces along the indicated isomorphism between

and

, and checking that the resulting space is still a covering space.
Now we can prove van Kampen’s theorem. Suppose that one has group homomorphisms

,

to a target group

which form a commuting square with the canonical homomorphisms from

to

and

. It will suffice to show that there is a unique homomorphism

such that

factors as the composition of
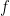
with the canonical homomorphism from

to

for

.
We first demonstrate existence. Let

be a universal cover for

, thus

is simply connected, and if we pick a base point

, then every other point
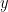
in that fibre there is a unique element

for which

, where

is the (right) action of
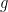
by
monodromy on

. This gives a left action of

on

by
deck transformations 
for each

, which maps

to

for any

:
The fibres of the universal cover

are copies of

. We can now form a new cover

whose fibres are copies of

, by first forming the Cartesian product

(which still covers

) and then quotienting out by the equivalence

for all
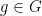
,

,

. This is a (possibly disconnected) covering space for

, whose fibre above
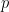
can be identified with

by identifying
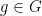
with the equivalence class
![{[(g, x_1)]} {[(g, x_1)]}](http://s0.wp.com/latex.php?latex=%7B%5B%28g%2C+x_1%29%5D%7D&bg=ffffff&fg=000000&s=0)
. The monodromy (right) action of

on this fibre is then identified with the right action of

on

induced by
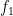
. Furthermore, the group

acts on

on the left by deck transformations, with each
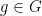
mapping
![{[(g',x)]} {[(g',x)]}](http://s0.wp.com/latex.php?latex=%7B%5B%28g%27%2Cx%29%5D%7D&bg=ffffff&fg=000000&s=0)
to
![{[(gg',x)]} {[(gg',x)]}](http://s0.wp.com/latex.php?latex=%7B%5B%28gg%27%2Cx%29%5D%7D&bg=ffffff&fg=000000&s=0)
.
Similarly, we can form a covering

of
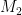
whose monodromy action of

on the fibre

can be identified with the right action of

on

induced by

. When both of these covering spaces are restricted to

, the monodromy action of

on the fibre above
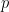
are then isomorphic to each other, and thus the two restrictions are isomorphic to each other too. By Proposition
2, we can then glue these two covers together to obtain a cover

which is isomorphic to
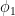
or

upon restricting the base to

or
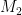
respectively, with all four isomorphisms forming a commuting square; in particular, the fibre

is still identified with

. The monodromy right action of

on

then restricts to the previously described action of

on

and of

on

. Also, because

acted on the left by deck transformations on both

and

, in a manner which can be seen to be compatible with the isomorphism on restriction to

,

continues to act by deck transformations on the gluid cover
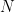
. As monodromy actions commute with deck transformations, we conclude that the right action of an element
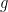
of

on

is given by right multiplication by an element

of

. It is then routine to verify that
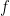
is a homomorphism with the required properties.
Now we prove uniqueness. It suffices to show that

is generated as a group by the images of

and

. Suppose this were not the case, so that the images of

and

generate a proper subgroup

of

. Let

be a universal cover of
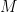
, so that the fibre

may be identified with

(after fixing a reference point in that fibre as before). Let

be the restriction of

to

. The monodromy (right) action of

on the fibre above
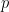
is induced by the canonical homomorphism from

to

. In particular,

is preserved by this action, and so one can find a proper subcover

of

whose fibre corresponds to

. Similarly, we can find a proper subcover

of the restriction

of

to
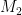
with the same fibre. By Proposition
2, we may glue these two covers together to obtain a proper subcover
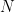
of

. But such a proper subcover cannot exist because

is connected, and the claim follows.
Remark 1 The arguments above relied heavily on the universal cover and its attendant deck transformations and monodromy actions, mostly in order to give a concrete equivalence between coverings of 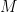 and discrete sets with actions of the fundamental group
and discrete sets with actions of the fundamental group  . It is also possible to proceed without constructing this cover, working instead with a directed family of Galois covers as a substitute for the universal cover to obtain this equivalence of categories; this is the approach in Grothendieck’s Galois theory, which among other things can be used to construct the étale fundamental group and establish its basic properties. See for instance Szamuely’s text for more details.
. It is also possible to proceed without constructing this cover, working instead with a directed family of Galois covers as a substitute for the universal cover to obtain this equivalence of categories; this is the approach in Grothendieck’s Galois theory, which among other things can be used to construct the étale fundamental group and establish its basic properties. See for instance Szamuely’s text for more details.
Filed under:
expository,
math.AT,
math.GN Tagged:
covering space,
fundamental group,
Grothendieck's Galois theory,
van Kampen's theorem 

DIGITAL JUICE
be connected open sets covering a connected topological manifold
with
also connected, and let
be an element of
. Then
is isomorphic to the amalgamated free product
.
be connected open sets covering a connected topological manifold
with
also connected, and let
be an element of
. If
and
are covering maps which become isomorphic upon restricting the base to
, then there is a covering map
which becomes isomorphic to
on restricting the base to
, and isomorphic to
on restricting the base to
(and with all four isomorphisms forming a commuting square).
and discrete sets with actions of the fundamental group
. It is also possible to proceed without constructing this cover, working instead with a directed family of Galois covers as a substitute for the universal cover to obtain this equivalence of categories; this is the approach in Grothendieck’s Galois theory, which among other things can be used to construct the étale fundamental group and establish its basic properties. See for instance Szamuely’s text for more details.
No comments:
Post a Comment
Thank's!