VizualBusiness: What are dense Sidon subsets of {1,2,…,n} like?

Friday, July 13, 2012

What are dense Sidon subsets of {1,2,…,n} like?

What are dense Sidon subsets of {1,2,…,n} like?:
The short answer if you don’t feel like reading a post with some actual mathematics in it is that I don’t know.
Now for the longer answer. A subset $A$ of $\{1,2,\dots,n\}$ is called a Sidon set if the only solutions of the equation $a+b=c+d$ with $a,b,c,d\in A$ are the trivial ones with $a=c$ and $b=d$ or $a=d$ and $b=c$ . Since the number of pairs $a\leq b$ with $a,b\in A$ is $|A|(|A|+1)/2$ and $2\leq a+b\leq 2n$ whenever $a,b\in A$ , it is trivial that if $A$ is a Sidon set, then $|A|(|A|+1)/2\leq 2n$ , which gives an upper bound for $|A|$ of around $2\sqrt{n}$ .

There is also a matching lower bound, up to a constant. I think it is due to ErdŎs. One notes first that the subset $\Gamma$ of $\mathbb{Z}_p^2$ defined by $\Gamma=\{(x,x^2):x\in\mathbb{Z}_p\}$ is a Sidon set inside $\mathbb{Z}_p^2$ . Indeed, if $(x,x^2)+(y,y^2)=(z,z^2)+(w,w^2)$ , then $x^2-z^2=w^2-y^2$ and $x-z=w-y$ . Assuming the quadruple is not degenerate, $x\ne z$ , so we can divide the first equation by the second to deduce that $x+z=w+y$ , and that implies that $x=w$ and $z=y$ , so the quadruple is degenerate for a different reason.
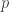
Thus, we can find a Sidon subset of $\mathbb{Z}_p^2$ of size $p$ , which is the square root of the size of $\mathbb{Z}_p^2$ . We can now regard this set as a subset of $\{0,1,\dots,p-1\}^2$ , and then map each point $(x,y)$ to the number $1+x+2py$ . It is easy to check that the resulting set is a Sidon subset of $\{1,2,\dots,2p^2\}$ .
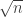
Much more is known about this: the correct bound is now known up to a constant. However, that is not the theme of this post. What I want to discuss is whether any kind of converse of this result is true. That is, can one say that a Sidon set of size close to $\sqrt{n}$ must be constructed in some kind of quadratic way?
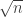
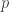
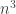
Some very weak evidence in favour of a conclusion like that is that random methods fail miserably to produce Sidon sets of anything like size $\sqrt{n}$ . Indeed, let’s pick a subset $A$ of $\{1,2,\dots,n\}$ randomly by choosing each element with probability $p$ . The total number of quadruples $x+y=z+w$ with $x,y,z,w$ taken from $\{1,2,\dots,n\}$ is roughly $n^3$ (since apart from a few edge effects $x,y$ and $z$ can be chosen more or less freely and they determine $w$ ), and each nondegenerate one has a probability $p^4$ . So the expected number of nondegenerate quadruples $x+y=z+w$ with $x,y,z,w\in A$ is roughly $p^4n^3$ . For this to be smaller than $|A|/2$ (so we can remove a point from each one and still have plenty of $A$ left), we need $p^4n^3$ to be significantly smaller than $pn$ , which gives a bound of $p=cn^{-2/3}$ , which gives us $|A|=cn^{1/3}$ .
There are several other ways to see that random sets of size $n^{1/2}$ are very different indeed from Sidon sets, which suggests that Sidon sets of size close to $n^{1/2}$ must have interesting structure. But what is that structure?
It isn’t easy even to state a conjecture here, since before we map the subset of $\mathbb{Z}_p^2$ to the integers, we can apply an invertible linear transformation to it. It is hard to think of a way of characterizing the kinds of sets that can arise like this, let alone thinking about how to make the structure looser when the set has size only $\sqrt{n}/1000$ . (Additive combinatorialists will immediately recognise that I am inspired by Freiman’s theorem here.)
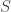
But today … make that yesterday as a night has passed since I wrote those two words … I was at a talk given by Javier Cilleruelo, thanks to which I learnt of an example that places a much more serious constraint on any conjecture one might hope to make. The example is one I sort of knew already, since it is based on a brilliant argument of Imre Ruzsa, who created an infinite Sidon set $S$ such that the asymptotic size of $S\cap\{1,2,\dots,n\}$ is around $n^{\sqrt{2}-1}$ . (As with the finite case, $n^{1/3}$ is very easy; the true answer is conjectured to be $n^{1/2-o(1)}$ ; Ruzsa was the first person to beat $n^{1/3+o(1)}$ and his exponent has not been improved.) What Cilleruelo mentioned in passing was that you can use some of Ruzsa’s ideas in an easy way to get a pretty decent example in the finite case. This is something I hadn’t realized. I presume Ruzsa himself was well aware of it, but I don’t remember it being mentioned in his paper (though I haven’t looked at the paper for many years, so he might have done). 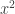What I find particularly interesting is that the example is completely different from the graph-of- $x^2$ type examples.
Since the construction is simple (to understand, that is) and rather gorgeous, I thought it merited a blog post. And maybe it can also serve as an advertisement for Ruzsa’s amazing paper.
It begins with the observation that the logarithms of the primes form a Sidon set of reals: if $p,q,r,s$ are primes with $pq=rs$ , then either $p=r$ and $q=s$ or $p=s$ and $q=r$ ; therefore, the same is true if $\log p+\log q=\log r+\log s$ .
“So what?” it is tempting to say. After all, the logs of the primes are not integers. Indeed, there are far more of them than there are integers.
However, at this point a principle comes in that I often feel doesn’t deserve to be as incredibly fundamentally useful as it in fact is: that two distinct integers must differ by at least 1. It’s not too much of an exaggeration to say, for example, that to prove that a concrete number is irrational or transcendental you have to find some way of reducing the problem to this principle. (That is, you say that if your number is rational/algebraic then there must be two distinct integers that have difference less than 1.) For this problem we make a much simpler use of the principle. If $pq\ne rs$ , then $|pq-rs|\geq 1$ , since $p,q,r,s$ are integers. Since the derivative of $\log x$ is $1/x$ , that tells us that $\log(pq)$ and $\log(rs)$ differ by at least $1/2pq$ . (One could be a bit more careful here: I think Cilleruelo stated a bound of $1/(pqrs)^{1/2}$ .)
Note what we now have that’s better: instead of merely knowing that $\log p+\log q\ne\log r+\log s$ in nondegenerate cases, we have a lower bound on the difference. This allows us to approximate and discretize.
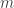
So let’s start with all the logs of the primes up to $m$ , of which there are about $m/\log m$ by the prime number theorem. If we multiply those by say $6m^2$ , then all the differences between the distinct sums, which were previously at least $1/2m^2$ , are now at least $3$ . Therefore, if we move each number to the nearest integer, the differences will be altered by at most 2, so will be at least 1. So we have a Sidon set! It is a subset of the integers up to $m^2\log m$ and it has size around $m/\log m$ , so this construction gives a Sidon subset of $\{1,2,\dots,n\}$ of size around $n^{1/2}/\log n$ .
The moral of this is that to prove a structural result about Sidon sets of density close to $n^{1/2}$ , then one would probably have to insist on close meaning “within a constant of” (which one would then relax to some slow-growing function later). Or alternatively, one would look for a much more general notion of structure, but I don’t see an obvious generalization of the two examples I now know. Another moral is that it’s worth looking for more examples of dense Sidon sets before even trying to make a conjecture.