A second experiment concerning mathematical writing.:
The time has come to reveal what the experiment in the previous post was about. As with many experiments (the most famous probably being that of Stanley Milgram about obedience to authority), its real purpose was not its ostensive purpose.
Over the last three years, I have been collaborating with Mohan Ganesalingam, a computer scientist, linguist and mathematician (and amazingly good at all three) on a project to write programs that can solve mathematical problems. We have recently produced our first program. It is rather rudimentary: the only problems it can solve are ones that mathematicians would describe as very routine and not requiring any ideas, and even within that class of problems there are considerable restrictions on what it can do; we plan to write more sophisticated programs in the future. However, each of the problems in the previous post belongs to the class of problems that it
can solve, and for each problem one write-up was by an undergraduate mathematician, one by a mathematics PhD student and one by our program. (To be clear, the program was given the problems and produced the proofs and the write-ups with no further help. I will have more to say about how it works in future posts.) We wanted to see whether anybody would suspect that not all the write-ups were human-generated. Nobody gave the slightest hint that they did.
Of course, there is a world of difference between not noticing a difference that you have not been told to look out for, and being unable to detect that difference at all. Our aim was merely to be able to back up a claim that our program produces passable human-style output, so we did not want to subject that output to full Turing-test-style scrutiny, but you may, if you were kind enough to participate in the experiment, feel slightly cheated. Indeed, in a certain sense you
were cheated — that was the whole point. It seems only fair to give you the chance to judge the write-ups again now that you know how they were produced. For each problem I have created a poll, and each poll has seven possible answers. These are:
The computer-generated output is definitely (a).
I think the computer-generated output is (a) but am not certain.
The computer-generated output is definitely (b).
I think the computer-generated output is (b) but am not certain.
The computer-generated output is definitely (c).
I think the computer-generated output is (c) but am not certain.
I have no idea which write-up was computer generated.
I would also be interested in comments about how you came to your judgments. All comments on both experiments and all votes in the polls will be kept private until I decide that it is time to finish the second experiment. A small remark is that I transcribed by hand all the write-ups into a form suitable for WordPress, so the existence of a typo in a write-up is not a trivial proof that it was by a human.
If you did not participate in the first experiment but nevertheless want to try this one, that’s fine.
Problem 1. Let

and
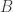
be open sets in a metric space. Then

is open.
1(a) We want to show that for all

in

, there exists

such that the open ball

is contained in

.
Let

.

is in

, so

is in

and

is in
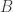
. Since

and
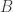
are open, there exist

such that

and

. Let

. Then

is contained in

, so it’s contained in

. Similarly,

is contained in

, so it’s contained in
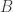
. So

. So

is open.
1(b) For arbitrary

, let

. Consider an arbitrary

. As

are open there are

such that

and

. Take

. Then

and

. So

. We’ve proved that for any

there is an open ball (

in this case) that contains

and is inside

. So

is open.
1(c) Let

be an element of

. Then

and

. Therefore, since

is open, there exists

such that

whenever

and since
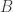
is open, there exists

such that

whenever

. We would like to find

s.t.

whenever

. But

if and only if

and

. We know that

whenever

and that

whenever

. Assume now that

. Then

if

and

if

. We may therefore take

and we are done.
Take Our Poll
Problem 2. Let
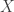
and

be metric spaces, let

be continuous, and let
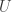
be an open subset of

. Then

is an open subset of
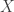
.
2(a) Let

be an element of

. Then

. Therefore, since
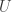
is open, there exists

such that

whenever

. We would like to find

s.t.

whenever

. But

if and only if

. We know that

whenever

. Since

is continuous, there exists

such that

whenever

. Therefore, setting

, we are done.
2(b) Let

. We seek

such that the open ball

is contained in

.

, so

.
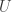
is open, so we know that for some

,

. Since

is continuous, there exists

such that for all

,

; i.e.,

. So

if

; i.e.,

. So

is open.
2(c) Take any

. We have

. As
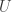
is open, there is an open ball

in
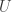
. Because

is continuous, there is some

such that for any

,

belongs to

. Hence, for such
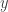
,

. So

. So

. We’ve proved that every point in

has an open ball neighbourhood. So

is open.
Take Our Poll
Problem 3. Let
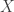
be a complete metric space and let

be a closed subset of
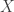
. Then

is complete.
3(a) Consider an arbitrary Cauchy sequence

in

. As
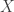
is complete,
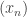
has a limit in
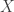
. Suppose

. Because

is closed,

belongs to

. We’ve proved that every Cauchy sequence in

has a limit point in

. So

is complete.
3(b) Let

be a Cauchy sequence in

. Then, since
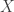
is complete, we have that

converges. That is, there exists

such that

. Since

is closed in
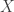
,

is a sequence in

and

, we have that

. Thus

converges in

and we are done.
3(c) Let

be a Cauchy sequence in

. We want to show that

tends to a limit in

.
Since

is a subset of
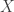
,

is a Cauchy sequence in
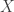
. Since
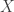
is complete,

, for some

. Since

is a closed subset of
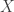
, it must contain all its limit points, so

. So

in

. So

is complete.
Take Our Poll
Problem 4. Let

and

be metric spaces and let

and

be continuous. Then the composition

is continuous.
4(a) Let

, and let

. We need to show that there exists

such that for all

,

.

is continuous, so there exists

such that for all

,

.

is continuous, so there exists

such that for all

,

. But then

, as desired. So

is continuous.
4(b) Take an arbitrary

. Let
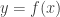
and

. Using continuity of

, for any

, there is some

such that if

(for

), then

. As

is continuous, there is some

such that if

(for

), then

. So for any

we’ve found

such that if

, then

and therefore

. Hence

is continuous.
4(c) Take

and

. We would like to find

s.t.

whenever

. Since

is continuous, there exists

such that

whenever

. Since

is continuous, there exists

such that

whenever

. Therefore, setting

, we are done.
Take Our Poll
Problem 5. Let
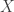
and

be sets, let

be an injection and let

and
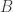
be subsets of
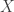
. Then

.
5(a) Take

. So there is some

and

such that

. As

is injective,
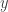
and

are equal. So

. So

.
5(b) Suppose

. Then, for some

,

and

. So

. Since

is injective,

, so

, so

. So

.
5(c) Let

be an element of

. Then

and

. That is, there exists

such that

and there exists

such that

. Since

is an injection,

and

, we have that

. We would like to find

s.t.

. But

if and only if

and

. Therefore, setting

, we are done.
Take Our Poll


DIGITAL JUICE
No comments:
Post a Comment
Thank's!