Orthogonal and Symplectic Lie Algebras:
For the next three families of
linear Lie algebras we equip our vector space

with a
bilinear form 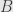
. We’re going to consider the endomorphisms
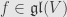
such that

If we pick a basis

of

, then we have a
matrix for the bilinear form
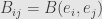
and one for the endomorphism

So the condition in terms of matrices in

comes down to

or, more abstractly,
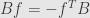
.
So do these form a subalgebra of
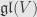
? Linearity is easy; we must check that this condition is closed under the bracket. That is, if

and

both satisfy this condition, what about their commutator
![[f,g] [f,g]](http://s0.wp.com/latex.php?latex=%5Bf%2Cg%5D&bg=e6e6e6&fg=333333&s=0)
?
,y)&=B(f(g(x))-g(f(x)),y)\\&=B(f(g(x)),y)-B(g(f(x)),y)\\&=-B(g(x),f(y))+B(f(x),g(y))\\&=B(x,g(f(y)))-B(x,f(g(y)))\\&=-B(x,f(g(y))-g(f(y)))\\&=-B(x,[f,g](y))\end{aligned} \displaystyle\begin{aligned}B([f,g](x),y)&=B(f(g(x))-g(f(x)),y)\\&=B(f(g(x)),y)-B(g(f(x)),y)\\&=-B(g(x),f(y))+B(f(x),g(y))\\&=B(x,g(f(y)))-B(x,f(g(y)))\\&=-B(x,f(g(y))-g(f(y)))\\&=-B(x,[f,g](y))\end{aligned}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cbegin%7Baligned%7DB%28%5Bf%2Cg%5D%28x%29%2Cy%29%26%3DB%28f%28g%28x%29%29-g%28f%28x%29%29%2Cy%29%5C%5C%26%3DB%28f%28g%28x%29%29%2Cy%29-B%28g%28f%28x%29%29%2Cy%29%5C%5C%26%3D-B%28g%28x%29%2Cf%28y%29%29%2BB%28f%28x%29%2Cg%28y%29%29%5C%5C%26%3DB%28x%2Cg%28f%28y%29%29%29-B%28x%2Cf%28g%28y%29%29%29%5C%5C%26%3D-B%28x%2Cf%28g%28y%29%29-g%28f%28y%29%29%29%5C%5C%26%3D-B%28x%2C%5Bf%2Cg%5D%28y%29%29%5Cend%7Baligned%7D&bg=e6e6e6&fg=333333&s=0)
So this condition will always give us a linear Lie algebra.
We have three different families of these algebras. First, we consider the case where
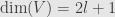
is odd, and we let
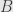
be the symmetric, nondegenerate bilinear form with matrix

where

is the

identity matrix. If we write the matrix of our endomorphism in a similar form

our matrix conditions turn into

From here it’s straightforward to count out

basis elements that satisfy the conditions on the first row and column,

that satisfy the antisymmetry for

, another

that satisfy the antisymmetry for

, and
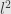
that satisfy the condition between

and

, for a total of

basis elements. We call this Lie algebra the orthogonal algebra of

, and write

or
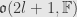
. Sometimes we refer to the isomorphism class of this algebra as

.
Next up, in the case where

is even we let the matrix of
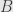
look like

A similar approach to that above gives a basis with

elements. We also call this the orthogonal algebra of

, and write

or

. Sometimes we refer to the isomorphism class of this algebra as
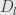
.
Finally, we again take an even-dimensional

, but this time we use the skew-symmetric form
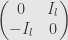
This time we get a basis with
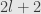
elements. We call this the symplectic algebra of

, and write

or

. Sometimes we refer to the isomorphism class of this algebra as

.
Along with the
special linear Lie algebras, these form the “classical” Lie algebras. It’s a tedious but straightforward exercise to check that for any classical Lie algebra

, each basis element

of

can be written as a bracket of two other elements of

. That is, we have
![[L,L]=L [L,L]=L](http://s0.wp.com/latex.php?latex=%5BL%2CL%5D%3DL&bg=e6e6e6&fg=333333&s=0)
. Since
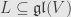
for some

, and since we know that
![[\mathfrak{gl}(V),\mathfrak{gl}(V)]=\mathfrak{sl}(V) [\mathfrak{gl}(V),\mathfrak{gl}(V)]=\mathfrak{sl}(V)](http://s0.wp.com/latex.php?latex=%5B%5Cmathfrak%7Bgl%7D%28V%29%2C%5Cmathfrak%7Bgl%7D%28V%29%5D%3D%5Cmathfrak%7Bsl%7D%28V%29&bg=e6e6e6&fg=333333&s=0)
, this establishes that
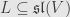
for all classical

.


DIGITAL JUICE
No comments:
Post a Comment
Thank's!