Tuesday, August 21, 2012

Nilpotent and Solvable Lie Algebras

Nilpotent and Solvable Lie Algebras:
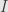
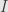
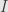
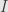
There are two big types of Lie algebras that we want to take care of right up front, and both of them are defined similarly. We remember that if I and J are ideals of a Lie algebra L, then [I,J] — the collection spanned by brackets of elements of I and J — is also an ideal of L. And since the bracket of any element of I with any element of L is back in I, we can see that [I,J]\subseteq I. Similarly we conclude [I,J]\subseteq J, so [I,J]\subseteq I\cap J.
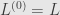
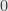
Now, starting from L we can build up a tower of ideals starting with L^{(0)}=L and moving down by L^{(n+1)}=[L^{(n)},L^{(n)}]\subseteq L^{(n)}. We call this the “derived series” of L. If this tower eventually bottoms out at 0 we say that L is “solvable”. If L is abelian we see that L^{(1)}=[L,L]=0, so L is automatically solvable. 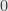At the other extreme, if L is simple — and thus not abelian — the only possibility is [L,L]=L, so the derived series never gets down to 0, and thus L is not solvable.
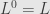
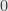
We can build up another tower, again starting with L^0=L, but this time moving down by L^{n+1}=[L,L^n]. We call this the “lower central series” or “descending central series” of L. If this tower eventually bottoms out at 0 we say that L is “nilpotent”. Just as above we see that abelian Lie algebras are automatically nilpotent, while simple Lie algebras are never nilpotent.
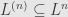
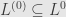
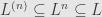
It’s not too hard to see that L^{(n)}\subseteq L^n for all n. Indeed, L^{(0)}\subseteq L^0 to start. Then if L^{(n)}\subseteq L^n\subseteq L then
\displaystyle\begin{aligned}L^{(n+1)}&\subseteq [L^{(n)},L^{(n)}]\\&\subseteq [L,L^n]\\&=L^{n+1}\end{aligned}
so the assertion follows by induction. Thus we see that any nilpotent algebra is solvable, but solvable algebras are not necessarily nilpotent.
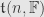
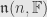
As some explicit examples, we look back at the algebras \mathfrak{t}(n,\mathbb{F}) and \mathfrak{n}(n,\mathbb{F}). The second, as we might guess, is nilpotent, and thus solvable. The first, though, is merely solvable.
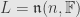
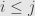
First, let’s check that L=\mathfrak{n}(n,\mathbb{F}) is nilpotent. The obvious basis consists of all the matrix entries e_{ij} with i\leq j, and we can know that
\displaystyle[e_{ij},e_{kl}]=\delta_{jk}e_{il}
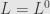
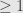
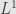
We have an obvious sense of the “level” of an element: the difference j-i, which is well-defined on each basis element. We can tell that the bracket of two basis elements gives either zero or another basis element whose level is the sum of the levels of the first two basis elements. The ideal L=L^0 is spanned by all the basis elements of level \geq1. The ideal L^1 is then spanned by basis elements of level \geq2. 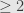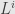And so it goes, each L^i spanned by basis elements of level \geq i+1. 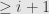But this must run out soon enough, since the highest possible level is n-1. 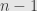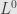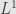In terms of the matrix, elements of L^0 are zero everywhere on or below the diagonal; elements of L^1 are also zero one row above the diagonal; and so on, each step pushing the nonzero elements “off the edge” to the upper-right of the matrix. 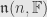Thus \mathfrak{n}(n,\mathbb{F}) is nilpotent, and thus solvable as well.
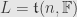
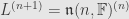
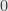
Turning to L=\mathfrak{t}(n,\mathbb{F}), we already know that L^{(1)}=[L,L]=\mathfrak{n}(n,\mathbb{F}), which we just showed to be solvable! We see that L^{(n+1)}=\mathfrak{n}(n,\mathbb{F})^{(n)}, which will eventually bottom out at 0, thus L is solvable as well. However, we can also calculate that
\displaystyle\begin{aligned}L^2&=[L,L^1]\\&=[\mathfrak{t}(n,\mathbb{F}),\mathfrak{n}(n,\mathbb{F})]\\&=\mathfrak{n}(n,\mathbb{F})\\&=L^1\end{aligned}
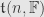
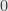
and so the derived series of \mathfrak{t}(n,\mathbb{F}) stops after the first term and never reaches 0. Thus this algebra is solvable, but not nilpotent.



DIGITAL JUICE
Posted by at

No comments:

Post a Comment

Thank's!

Subscribe to: Post Comments (Atom)