Multiple recurrence in quasirandom groups:
I’ve just uploaded to the arXiv my joint paper with
Vitaly Bergelson, “
Multiple recurrence in quasirandom groups“, which is submitted to
Geom. Func. Anal.. This paper builds upon a
paper of Gowers in which he introduced the concept of a
quasirandom group, and established some mixing (or recurrence) properties of such groups. A
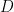
-quasirandom group is a finite group with no non-trivial unitary representations of dimension at most
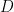
. We will informally refer to a “quasirandom group” as a
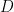
-quasirandom group with the quasirandomness parameter
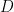
large (more formally, one can work with a
sequence of

-quasirandom groups with

going to infinity). A typical example of a quasirandom group is
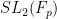
where
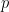
is a large prime. Quasirandom groups are discussed in depth in
this blog post. One of the key properties of quasirandom groups established in Gowers’ paper is the following “weak mixing” property: if
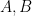
are subsets of

, then for “almost all”
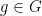
, one has
where
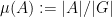
denotes the density of
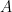
in

. Here, we use
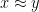
to informally represent an estimate of the form
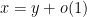
(where

is a quantity that goes to zero when the quasirandomness parameter
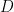
goes to infinity), and “almost all
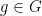
” denotes “for all
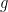
in a subset of

of density
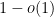
“. As a corollary, if

have positive density in

(by which we mean that

is bounded away from zero, uniformly in the quasirandomness parameter
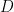
, and similarly for
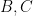
), then (if the quasirandomness parameter
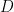
is sufficiently large) we can find elements

such that

,

,

. In fact we can find approximately
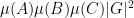
such pairs

. To put it another way: if we choose
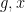
uniformly and independently at random from

, then the events

,

,

are approximately independent (thus the random variable

resembles a uniformly distributed random variable on

in some weak sense). One can also express this mixing property in integral form as
for any bounded functions

. (Of course, with

being finite, one could replace the integrals here by finite averages if desired.) Or in probabilistic language, we have
where

are drawn uniformly and independently at random from

.
As observed in Gowers’ paper, one can iterate this observation to find “parallelopipeds” of any given dimension in dense subsets of

. For instance, applying
(1) with

replaced by

,

, and
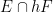
one can assert (after some relabeling) that for
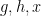
chosen uniformly and independently at random from

, the events

,
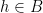
,
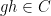
,

,

,

,

are approximately independent whenever
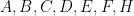
are dense subsets of

; thus the tuple

resebles a uniformly distributed random variable in
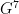
in some weak sense.
However, there are other tuples for which the above iteration argument does not seem to apply. One of the simplest tuples in this vein is the tuple
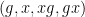
in

, when

are drawn uniformly at random from a quasirandom group

. Here, one does
not expect the tuple to behave as if it were uniformly distributed in

, because there is an obvious constraint connecting the last two components

of this tuple: they must lie in the same conjugacy class! In particular, if
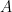
is a subset of

that is the union of conjugacy classes, then the events
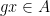
,
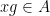
are perfectly correlated, so that

is equal to

rather than

. Our main result, though, is that in a quasirandom group, this is (approximately) the
only constraint on the tuple. More precisely, we have
Theorem 1 Let  be a
be a 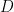 -quasirandom group, and let
-quasirandom group, and let  be drawn uniformly at random from
be drawn uniformly at random from  . Then for any
. Then for any ![{f_1,f_2,f_3,f_4: G \rightarrow [-1,1]} {f_1,f_2,f_3,f_4: G \rightarrow [-1,1]}](http://s0.wp.com/latex.php?latex=%7Bf_1%2Cf_2%2Cf_3%2Cf_4%3A+G+%5Crightarrow+%5B-1%2C1%5D%7D&bg=ffffff&fg=000000&s=0) , we have
, we have
where  goes to zero as
goes to zero as  ,
, 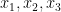 are drawn uniformly and independently at random from
are drawn uniformly and independently at random from  , and
, and  is drawn uniformly at random from the conjugates of
is drawn uniformly at random from the conjugates of  for each fixed choice of
for each fixed choice of 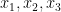 .
.
This is the probabilistic formulation of the above theorem; one can also phrase the theorem in other formulations (such as an integral formulation), and this is detailed in the paper. This theorem leads to a number of recurrence results; for instance, as a corollary of this result, we have
for almost all
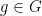
, and any dense subsets
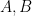
of

; the lower and upper bounds are sharp, with the lower bound being attained when
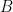
is randomly distributed, and the upper bound when
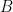
is conjugation-invariant.
To me, the more interesting thing here is not the result itself, but how it is proven. Vitaly and I were not able to find a purely finitary way to establish this mixing theorem. Instead, we had to first use the machinery of ultraproducts (as discussed in
this previous post) to convert the finitary statement about a quasirandom group to an infinitary statement about a type of infinite group which we call an
ultra quasirandom group (basically, an ultraproduct of increasingly quasirandom finite groups). This is analogous to how the Furstenberg correspondence principle is used to convert a finitary combinatorial problem into an infinitary ergodic theory problem.
Ultra quasirandom groups come equipped with a finite, countably additive measure known as
Loeb measure 
, which is very analogous to the Haar measure of a compact group, except that in the case of ultra quasirandom groups one does not quite have a topological structure that would give compactness. Instead, one has a slightly weaker structure known as a
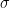 -topology
-topology, which is like a topology except that open sets are only closed under countable unions rather than arbitrary ones. There are some interesting measure-theoretic and topological issues regarding the distinction between topologies and
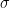
-topologies (and between Haar measure and Loeb measure), but for this post it is perhaps best to gloss over these issues and pretend that ultra quasirandom groups

come with a Haar measure. One can then recast Theorem
1 as a mixing theorem for the left and right actions of the ultra approximate group

on itself, which roughly speaking is the assertion that
for “almost all”
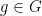
, if

are bounded measurable functions on

, with
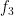
having zero mean on all conjugacy classes of

, where
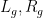
are the left and right translation operators
To establish this mixing theorem, we use the machinery of
idempotent ultrafilters, which is a particularly useful tool for understanding the ergodic theory of actions of countable groups

that need not be amenable; in the non-amenable setting the classical ergodic averages do not make much sense, but ultrafilter-based averages are still available. To oversimplify substantially, the idempotent ultrafilter arguments let one establish mixing estimates of the form
(2) for “many” elements
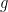
of an infinite-dimensional parallelopiped known as an
IP system (provided that the actions
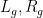
of this IP system obey some technical mixing hypotheses, but let’s ignore that for sake of this discussion). The claim then follows by using the quasirandomness hypothesis to show that if the estimate
(2) failed for a large set of
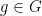
, then this large set would then contain an IP system, contradicting the previous claim.
Idempotent ultrafilters are an extremely infinitary type of mathematical object (one has to use Zorn’s lemma no fewer than
three times just to construct one of these objects!). So it is quite remarkable that they can be used to establish a finitary theorem such as Theorem
1, though as is often the case with such infinitary arguments, one gets absolutely no quantitative control whatsoever on the error terms

appearing in that theorem. (It is also mildly amusing to note that our arguments involve the use of ultrafilters in two completely different ways: firstly in order to set up the ultraproduct that converts the finitary mixing problem to an infinitary one, and secondly to solve the infinitary mixing problem. Despite some superficial similarities, there appear to be no substantial commonalities between these two usages of ultrafilters.) There is already a fair amount of literature on using idempotent ultrafilter methods in infinitary ergodic theory, and perhaps by further development of ultraproduct correspondence principles, one can use such methods to obtain further finitary consequences (although the state of the art for idempotent ultrafilter ergodic theory has not advanced much beyond the analysis of two commuting shifts
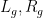
currently, which is the main reason why our arguments only handle the pattern

and not more sophisticated patterns).
We also have some miscellaneous other results in the paper. It turns out that by using the
triangle removal lemma from graph theory, one can obtain a recurrence result that asserts that whenever
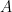
is a dense subset of a finite group

(not necessarily quasirandom), then there are
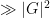
pairs

such that

all lie in
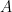
. Using a hypergraph generalisation of the triangle removal lemma known as the
hypergraph removal lemma, one can obtain more complicated versions of this statement; for instance, if
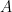
is a dense subset of

, then one can find
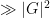
triples

such that

all lie in
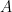
. But the method is tailored to the specific types of patterns given here, and we do not have a general method for obtaining recurrence or mixing properties for arbitrary patterns of words in some finite alphabet such as
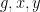
.
We also give some properties of a model example of an ultra quasirandom group, namely the ultraproduct

of

where

is a sequence of primes going off to infinity. Thanks to the substantial recent progress (by Helfgott, Bourgain, Gamburd, Breuillard, and others) on understanding the expansion properties of the finite groups

, we have a fair amount of knowledge on the ultraproduct

as well; for instance any two elements of

will almost surely generate a spectral gap. We don’t have any direct application of this particular ultra quasirandom group, but it might be interesting to study it further.
Filed under:
math.CO,
math.DS,
math.GR,
paper Tagged:
quasirandom groups,
ultrafilters,
ultraproducts,
Vitaly Bergelson 

DIGITAL JUICE






