If
is a module of a Lie algebra 
, there is one submodule that turns out to be rather interesting: the submodule 
of vectors 
such that 
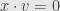
for all 
. We call these vectors “invariants” of .As an illustration of how interesting these are, consider the modules we looked at last time. What are the invariant linear maps
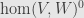
from one module to another 
? We consider the action of on a linear map 
:=x\cdot f(V)-f(x\cdot v)=0](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cleft%5Bx%5Ccdot+f%5Cright%5D%28v%29%3Dx%5Ccdot+f%28V%29-f%28x%5Ccdot+v%29%3D0&bg=e6e6e6&fg=333333&s=0 "\displaystyle\left[x\cdot f\right](v)=x\cdot f(V)-f(x\cdot v)=0")
Or, in other words:
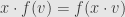
That is, a linear map
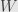
is invariant if and only if it intertwines the actions on and . That is, 
.Next, consider the bilinear forms on
. Here we calculate&=-B([y,x],z)-B(x,[y,z])\\&=B([x,y],z)-B(x,[y,z])=0\end{aligned}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cbegin%7Baligned%7D%5Cleft%5By%5Ccdot+B%5Cright%5D%28x%2Cz%29%26%3D-B%28%5By%2Cx%5D%2Cz%29-B%28x%2C%5By%2Cz%5D%29%5C%5C%26%3DB%28%5Bx%2Cy%5D%2Cz%29-B%28x%2C%5By%2Cz%5D%29%3D0%5Cend%7Baligned%7D&bg=e6e6e6&fg=333333&s=0 "\displaystyle\begin{aligned}\left[y\cdot B\right](x,z)&=-B([y,x],z)-B(x,[y,z])\\&=B([x,y],z)-B(x,[y,z])=0\end{aligned}")
That is, a bilinear form is invariant if and only if it is associative, in the sense that the Killing form is:
![B([x,y],z)=B(x,[y,z])](http://s0.wp.com/latex.php?latex=B%28%5Bx%2Cy%5D%2Cz%29%3DB%28x%2C%5By%2Cz%5D%29&bg=e6e6e6&fg=333333&s=0 "B([x,y],z)=B(x,[y,z])")
DIGITAL JUICE
No comments:
Post a Comment
Thank's!