EDP26 — three generalizations:
This short post is designed as a possible way in to EDP for anyone who might be interested in participating but daunted by the idea of reading large amounts of material. One of the natural strategies for proving EDP is to try to formulate and prove stronger statements. At first that sounds paradoxical: isn’t it even harder to prove a stronger statement? But the answer to that question is often no. To give a slightly silly example, suppose you were asked to prove that for every
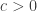
there exists
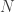
such that for every

if
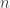
is odd and has at least
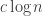
prime factors (counted with multiplicity), then

mod
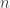
, where

is Euler’s totient function. You could make the problem easier by proving Euler’s theorem, that
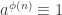
mod
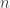
for every
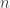
and every

that is coprime to
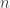
. You wouldn’t have as many hypotheses to use, but that’s good, since they can’t be used. Perhaps a better and more relevant example is when you generalize the class of numbers you are working with so as to allow a wider set of methods. For instance, suppose you want to prove that the largest possible product of three positive integers that add to 300 is at most
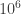
. If you replace positive integers by positive reals, then you suddenly have available methods that you didn’t have before — for example, you could use compactness plus a lemma that says that if any two numbers are not equal then you can increase the product by replacing both of them by their average. (I’m not saying that’s the easiest proof — just that it’s a proof that you can’t do without first generalizing the statement.)
In this post I want to mention three strengthenings of EDP. One of them I find interesting but not promising as a way of proving EDP, for reasons that I will explain. The other two look to me also very interesting and much more promising. All of them have been mentioned already, but the point of this post is to collect them in one convenient place.
Restricting the allowable common differences.
I know of no
-sequence that has bounded discrepancy on all HAPs with common difference either a prime or a power of 2. The sequence
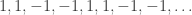
has bounded discrepancy on all HAPs of prime common difference, but if you allow powers of 2 as well, then no periodic construction can work, since if the period
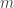
is
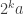
for some odd integer

, then a HAP of common difference
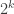
will have a bias of at least 1 in each interval of length
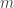
, for parity reasons, and this bias will gradually accumulate.
One can defeat powers of 2 by using the Morse sequence

(if you haven’t seen it, then it’s a nice exercise to see how it is generated), but that has unbounded discrepancy on HAPs of odd prime length. (I can’t remember exactly why.)
Why do I not think that this potential strengthening of EDP is likely to be useful for attacking the problem? Well, one promising feature of EDP is that it seems to generalize to sequences taking other kinds of values, such as complex numbers of modulus 1 or even unit vectors in an arbitrary Hilbert space. However, something that I’ve only just noticed (though others may have spotted it ages ago) is that if one restricts to, say, prime-power common differences, then even the complex version of the problem becomes false. A very simple counterexample is the sequence
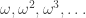
, where

(that is, a primitive sixth root of 1). Then the sum along any HAP with common difference

that isn’t a multiple of 6 will be a sum of a GP with common ratio

, and will therefore be (uniformly) bounded. In particular, this is true of HAPs with prime-power common difference.
This simple example also shows that a certain real generalization of EDP is false when you restrict the common differences in this way: you cannot prove unbounded discrepancy for sequences that take values in the set

. The counterexample is simply twice the real part of the example above: the sequence

repeated over and over again. So if (and I think it’s a big if) EDP is true for HAPs with common differences that are either primes or powers of 2, then any proof must make pretty strong use of the fact that the sequence is a
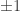
-valued sequence. This rules out a lot of promising techniques, so it appears to make the problem harder rather than easier.
A discrepancy question about matrices.
In my earlier post I mentioned what I called the non-symmetric vector-valued EDP. I have subsequently realized (though perhaps a better word is “remembered” since I must have been sort of aware of this at some point) that it is equivalent to another discrepancy statement that I now find more appealing. The statement is the following.
Conjecture. Let
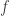
be a function from

to

and suppose that

for every
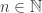
. Then for every real number
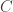
there exist HAPs
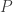
and

such that
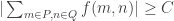
.
If we take a function
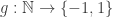
and define
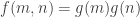
, then for every
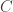
the above conjecture, if true, gives us HAPs
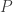
and

such that
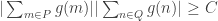
, which proves that the discrepancy of
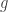
is at least

. So the above conjecture implies EDP. But the class of functions of the form
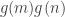
with
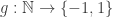
is a very small subset of the class of all functions
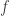
that take the value 1 along the diagonal, so this conjecture is very much stronger than EDP.
It is also equivalent to the statement that for every
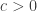
there exists a diagonal matrix
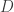
of trace at least 1 that can be written as a linear combination
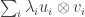
, where for each


and
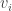
are characteristic functions of HAPs
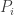
and
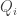
and
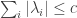
. (This is the statement that I discussed at length in my previous post.) In one direction this is easy: if a decomposition of that kind exists, then
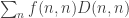
equals the trace of
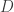
and is therefore greater than 1, but it also equals
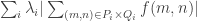
, which is at most
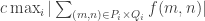
. It follows that there is some

such that
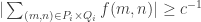
.
In the other direction, if no such decomposition of a diagonal matrix exists, then the Hahn-Banach theorem gives us a linear functional that separates the class of diagonal matrices with trace at least 1 from the class of linear combinations of HAP products defined above. It is easy to check that this functional must be a diagonal matrix

with a constant diagonal such that the value along the diagonal is at least 1 and such that

for any two HAPs
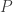
and

.
The conjecture is so much stronger than EDP that I think it would be a mistake just to assume that it is true. My guess is that it
is true, but I would be very interested if there was a counterexample (even if, like the complex sequence above, it is disappointingly simple — in fact, if there is a counterexample, then it seems quite likely that it will be fairly simple). And if there isn’t a counterexample, then the fact that it is so much stronger a conjecture than EDP does this time make me think that the result might be easier to prove than EDP itself.
Until very recently, I had been mainly interested in the dual version of the question (that is, the question about decomposing diagonal matrices), but now it seems to me that the matrix discrepancy question is worth thinking about directly. It is a clean question, and it has the big advantage over the original EDP question that it does not restrict values to the set
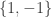
, so a number of methods can be used that cannot be used directly for EDP. For instance, linear programming can be used to get experimental results: Sasha Nikolov may be going to look into this.
Given any matrix
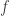
, one can find vectors

and

such that
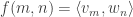
, so this matrix question is actually trivially equivalent to the non-symmetric vector-valued question I had formulated earlier. But expressing it in terms of vectors makes it harder to think about rather than easier, and that is what had previously put me off thinking about the question directly.
There is one class of matrices that is particularly worth mentioning I think. If EDP is true but this matrix question is false, then the best candidates for counterexamples to the matrix problem are probably matrices of high rank, and an obvious class of matrices that tend to have high rank is matrices that are constant on diagonals (that is,
Toeplitz matrices).
Suppose, then, that our matrix

is defined to be
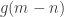
for some function
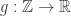
such that

. Then

, where by
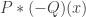
I mean the number of ways of writing

as
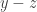
with
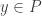
and

. So we have a class of functions that I’ll call
HAP convolutions, and we’d like to show that if
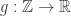
is any function with

and
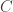
is any constant, then there exists a HAP convolution

such that
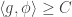
. This is true if and only if there is an efficient way of writing the function that is 1 at 0 and 0 everywhere else as a linear combination of HAP convolutions. This is another question that could be investigated using linear programming, and perhaps since it concerns functions of just one variable we could get more extensive results than we could for the general matrix problem.
The modular conjecture.
In his most recent guest post, Gil Kalai reformulates EDP as a question about sums mod
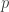
. EDP is trivially equivalent to the following assertion.
Conjecture. For every
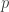
there exists
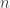
such that for every
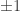
sequence

of length
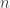
and every

there exists a HAP
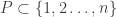
such that

mod
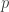
.
At first that doesn’t look like a very interesting reformulation since it is too obviously equivalent to EDP. But what makes it interesting is that it has a very natural generalization that doesn’t have any obvious counterexamples.
Stronger Conjecture. For every
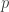
there exists
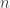
such that for every sequence

of length
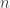
of non-zero numbers mod
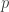
and every

there exists a HAP
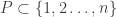
such that
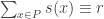
mod
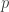
.
In other words, we replace the condition that the sequence takes values
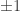
by the much weaker condition that it is never zero. Gil calls this the
modular conjecture. (He also presented it in a comment on a much earlier EDP post.)
As Gil points out in his post, one can write down a polynomial that is identically zero (mod
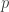
) if and only if the modular conjecture is true for
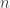
. It is tempting to try to prove that it is zero by analysing its coefficients. More generally, this approach to the problem appears to open the door to a number of algebraic methods.
If you want to prove EDP this way, you have to solve the conjecture for some non-zero

. (Since
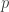
is prime, if you can show it for one then you’ve shown it for all.) However, the problem with
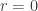
is interesting in its own right, and in particular it seems to be interestingly different from the problem with non-zero

. At the time of writing, I don’t see any way of modifying the EDP examples to obtain exponentially long sequences mod
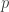
that avoid zero sums — it seems to me that the upper bound on the length could be significantly smaller. That would be interesting, as it would place constraints on what a proof could look like for non-zero

.
A fourth strengthening.
This isn’t really meant as part of the body of the post, but more of an afterthought. A strengthening of EDP that has been considered since very early on in the project is where you replace a
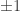
sequence by a sequence of unit vectors in a Hilbert space. To be precise, one looks at the following statement.
Conjecture. Let
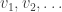
be a sequence of unit vectors in a Hilbert space and let
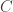
be a real number. Then there exists a HAP
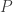
such that

.
There is something slightly curious about this conjecture, which is that it is very hard to see how having infinitely many dimensions to play with could help one find a counterexample. In some sense, if you use too many dimensions, then it ought to be the case that there will be a HAP
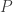
such that the vectors
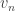
with
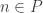
are pointing in lots of different directions and therefore not cancelling. That makes me wonder whether one can prove that if there is a counterexample to the above conjecture, then there must be a counterexample for some finite-dimensional Hilbert space. Or if that is too much to ask, perhaps there might have to be a counterexample where all the
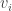
live in some compact set. I think it would be very interesting to think about whether the vague intuition I have just expressed can be made precise. As it stands, it is of course not even close to a proper argument. (I should stress one aspect of what I am saying. If there is any vector sequence
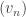
of bounded discrepancy, then one can arbitrarily modify

for each prime
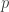
and the sequence will still have bounded discrepancy. So I’m not suggesting that every bounded-discrepancy sequence lives, or almost lives, in finite dimensions, but that it can be used to construct one that does.)
As I write that, another question occurs to me. For this one I don’t even have a vague intuitive argument. Let’s suppose that we can find a counterexample
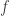
to the matrix discrepancy question earlier. Suppose also that

takes the form
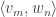
for some (not necessarily unit) vectors

and

in a Hilbert space. Must there be an example where the

and

lie in a finite-dimensional Hilbert space, or at least in a compact subset of a Hilbert space?
A combined generalization.
A second afterthought is that the matrix question has a modular version that might be of some interest. Let
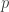
be a prime and let
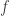
be a function from

to
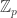
with

for every
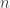
. Must the sums of
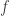
on products
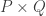
take all possible values mod
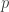
? What if we merely ask for
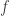
to take non-zero values on the diagonal?
If the strong modular conjecture is false, then we can turn a counterexample
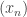
into a diagonal matrix in the obvious way and we get a counterexample to the second question. Indeed, suppose that

for every
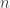
and
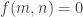
when
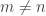
. Then
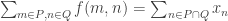
, which avoids some value, since
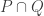
is a HAP. But with matrices there are many more ways of trying to avoid particular values, so the strong modular matrix conjecture looks like a much stronger statement. Again there are two cases — avoiding 0 and avoiding a non-zero value — of which only the second obviously implies EDP.


DIGITAL JUICE
No comments:
Post a Comment
Thank's!