Special Linear Lie Algebras

Special Linear Lie Algebras:
More examples of Lie algebras! Today, an important family of linear Lie algebras.
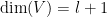
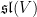
Take a vector space with dimension and start with . Inside this, we consider the subalgebra of endomorphisms whose trace is zero, which we write and call the “special linear Lie algebra”. This is a subspace, since the trace is a linear functional on the space of endomorphisms:

so if two endomorphisms have trace zero then so do all their linear combinations. It’s a subalgebra by using the “cyclic” property of the trace:

Note that this does not mean that endomorphisms can be arbitrarily rearranged inside the trace, which is a common mistake after seeing this formula. Anyway, this implies that

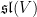
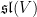
so actually not only is the bracket of two endomorphisms in back in the subspace, the bracket of any two endomorphisms of lands in . In other words: .
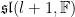
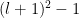
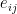
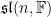
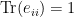
Choosing a basis, we will write the algebra as . It should be clear that the dimension is , since this is the kernel of a single linear functional on the -dimensional , but let’s exhibit a basis anyway. All the basic matrices with are traceless, so they’re all in . Along the diagonal, , so we need linear combinations that cancel each other out. It’s particularly convenient to define

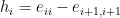
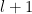
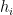
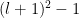
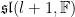
So we’ve got the basic matrices, but we take away the along the diagonal. Then we add back the new matrices , getting matrices in our standard basis for , verifying the dimension.
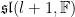
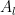
We sometimes refer to the isomorphism class of as . Because reasons.

DIGITAL JUICE